[전기자기학] 전계의 특수 해법 및 전류

전기영상법

 

▶  전기영상법이란?

- 전하가 1개만 존재하여 쿨롱의 힘을 직접 구하지 못하는 경우에 사용.

  ◇ 쿨롱의 법칙 : $F=\frac{1}{4\pi {\epsilon }_0}\cdot \frac{Q_1\cdot Q_2}{r^2}N]=9\times {10}^9\cdot \frac{Q_1{Q}_2}{r^2}$

- 임의의 가상전하를 놓고 해석

- 가상전하(영상전하)는 실제전하와 극성이 항상 반대임.

 

 

▶ 전기 영상법 6가지

 

1. 무한평면(=대지=기준) 과 과 점전하

1) 점전하 Q[C]에 대한 영상전하 -Q[C]이다.

    영상전하수 = $\frac{360}{\theta }-1$ 개 이다.

2) 작용력(흡인력)  $F=\frac{Q\times (-Q)}{4\pi {\epsilon }_0(2d{)}^2}=\frac{-Q^2}{16\pi {\epsilon }_0{d}^2}[N]$

3) 무한평면 임의점전위  $V=\frac{Q}{4\pi {\epsilon }_{0}r}+\frac{-Q}{4\pi {\epsilon }_{0}r}=0[V]$

4) $E_1=E_2=\frac{Q}{4\pi {\epsilon }_0{d}^2}[v/m]$ 인 원점에 전계 세기

    $E=E_1+E_2=\frac{Q}{4\pi {\epsilon }_0{d}^2}\times 2=\frac{Q}{2\pi {\epsilon }_0{d}^2}[v/m]$

5) 원점에서 전하밀도 = 최대유기 전하밀도

     $D_{max}={\sigma }_{max}=-{\epsilon }_{0}E=-\frac{Q}{2\pi d^2}[c/m^2]$

 

 

2. 직교도체 평면과 점전하

- 직교도체($\theta ={90}^{\circ }$) 평면과 점전하 사이에 영상전하수 = $\frac{360}{90}-1=3$개

 

3. 접지구 도체와 점전하

- 접지된 구도체와 점전하간에 작용하는 힘은 항상 흡인력이 작용된다.

- 반지름 a[m]인 접지구 도체와 점전하 사이에 영상전하 1개

   $\therefore$ 영상전하 $P^{\prime }=-\frac{a}{d}Q[C]$

   표피효과두께($\delta$) = $\sqrt{\frac{2}{\omega \mu \sigma }}=\frac{1}{\sqrt{\pi f\mu \sigma }}$

 

   - f=주파수 / $\mu$=투자율 / $\sigma$=도전율

 

 - f,$\mu$,$\sigma$ 증가, $\delta$값 감소, 표피효과 증가(크다)

 - f,$\mu$,$\sigma$ 감소, $\delta$값 증가, 표피효과 감소(작다)

 

4. 구도체가 부착된 무한평면과 점전하

- 구도체가 부착된 무한평면과 점전하 사이에 영상전하수 3개

 

$P^{\prime }=-Q$, $P^{″}=-\frac{a}{d}Q$, $P^{‴}=\frac{a}{d}Q$ 이다.

 

5. 유전체구와 점전하

- 유전율 ${\epsilon }_1[F/m]$, ${\epsilon }_2[F/m]$인 유전체구와 점전하 사이에 영상전하수 2개

 

$P^{\prime }=\frac{{\epsilon }_1-{\epsilon }_2}{{\epsilon }_1+{\epsilon }_2}q$, $P^{″}=\frac{2{\epsilon }_2}{{\epsilon }_1+{\epsilon }_2}q$

 

$F$(작용력)=$\frac{\frac{{\epsilon }_1-{\epsilon }_2}{{\epsilon }_1+{\epsilon }_2}{q}^2}{4\pi {\epsilon }_1(2r{)}^2}$

 

6. 구형기포

 

전계 세기 : $E^{\prime }=\frac{3{\epsilon }_1}{2{\epsilon }_1+{\epsilon }_2}{E}_0[v/m]$

 

분극 세기 : $P^{\prime }=\frac{3{\epsilon }_1({\epsilon }_2-{\epsilon }_1)}{2{\epsilon }_1+{\epsilon }_2}{E}_0[c/m^2]$

 

전속 밀도 : $D^{\prime }=\frac{3{\epsilon }_2}{2{\epsilon }_1+{\epsilon }_2}{D}_0[c/m^2]$

 

 

전류에 관련된 제현상

 

1. 전류와 전류밀도

1) 전류란?

- 공간적 개념 없이 점(0차원), 선(1차원)을 통해 전하가 흐른다는 시간 위주의 개념.

- 단위시간에 이동도히는 전기량

- 전류 : $I=\frac{Q}{t}[c/sec]=[A]$

- 전기량 : $Q=It[C]$

- 자유전자수 : $N=\frac{Q}{e}[EA]$

- $\therefore$ $1[C]=\frac{1}{1.602\times {10}^{-19}}\fallingdotseq 6.25\times {10}^{18}$

 

 

2) 전류 밀도란?

- 2차원, 3차원 공간을 통해 전하가 흐르는 개념.

- 전류밀도 J : 단위 시간 당 단위 면적을 통과하는 순 전하 흐름.

- 전류밀도 : $i=i_{c}+i_{d}=KE+\frac{ \partial D}{ \partial t}[A/m^{2}]$

- 전도 전류 : $i_c$

   - 도체 내에 흐르는 전류

   - 자유전자 이동에 의한 전류

   - 옴법칙 미분형 : 자유전자수 $n=\frac{Q}{e}$,  전자의 이동도$\mu =\frac{V}{E}$

 - 변위 전류 : $i_d$

   - 도체 외에 흐르는 전류

   - 구속전자 변위에 의한 전류

   - 전속밀도의 시간적인 변화에 의한 전류

 

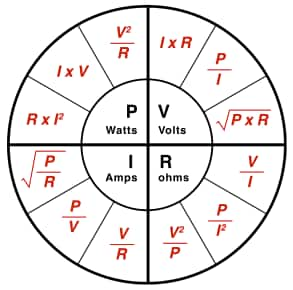
2. 옴의 법칙

출처 : Digikey

 

 

3. 키르히호프 법칙

1) 키르히호프 제 1법칙 (전류법칙)

- 연속성이다.

- 마디 전압을 구하는 식이다.

- 마디 중심에 들어가는 전류는 밖으로 나가는 전류와 서로 같다.

- 전류가 흐르는 분기점에서의 전류의 합은 0이다.

- 도선망(회로)안에서 전류의 대수적 합은 0이다.

 

2) 키르히호프 제 2법칙 (전압법칙)

- 폐회로 전류(망전류)를 구하는 식이다.

- 폐회로에서 기전력의 합은 전압강하의 힘과 서로 같다.

- 폐회로의 루프안 전압의 합은 0이다.

- 폐회로에 인가된 전원의 합과 분배된 전위의 차의 합은 그 루프 안에서 등가한다.

- 하나의 루프 안에서 도체에 인가된 전압의 대수의 합과 공급된 전압의 합은 같다.

 

4. 중첩의 원리

- 고정적인 전압/전류원이 둘 이상일 경우 하나만 남겨놨다고 가정하였을 때, 각 지점에서의 전압/전류의 값들의 총 합은 원래의 회로의 전압/전류의 값이 된다.

- 전압원 계산 시 전류원은 Open(개방) 상태로 보고 계산한다.

- 전류원 계산 시 전압원은 Short(단락) 상태로 보고 계산한다.

 

5. 상반(가역) 정리

- 단일 전원에서 적용되는 정리.

- 어떤 회로의 임의의 분기점 P에 기전력 E를 인가하였을 때 다른 분기점 Q에 흐르는 전류가 $I_Q$이고, 반대로 같은 기전력 E를 분기점 Q에 인가하였을 때 P점에 흐르는 전류가 $I_P$일 때 $I_P$와 $I_Q$가 같으면 성립하는 정리.

 

6. 등가 전원 정리

1) 테브난 정리

- 2개의 독립된 회로망을 접속하였을 때의 전압, 전류, 임피던스의 관계를 나타내는 정리

- 임의의 선형 2단자 회로망은 테브난 전압원 $V_{TH}$와 테브난 저항 $R_{TH}$를 직렬연결한 등가회로로 대체할 수 있다.

- 부하저항과 연결된 복잡한 회로가 있을 때, 부하저항을 제외한 나머지 회로를 하나의 전압원과 저항으로 바꾸는 기술.

- $V_{TH}$ 는 부하저항을 개방한 상태에서 부하 양단에 걸리는 전압.

- $R_{TH}$ 는 회로에서 전압원을 단락시키고, 부하쪽에서 회로쪽을 바라본 저항.

 

2) 노튼의 정리

- 임의의 선형 2단자 회로망을 노턴의 등가전류원 $I_N$과 노턴의 등가저항 $R_N$을 병렬로 연결한 등가회로로 대체할 수 있다.

- 부하저항을 없애고, 그 자리를 단락시킨다. 이 단락된 곳에 흐르는 전류를 계산하면 그 전류가 노턴의 등가전류인 $I_N$이 된다. 

- 부하저항 $R_L$을 제거하고, 회로쪽을 바라본 저항이 노턴의 등가저항 $R_N$인데, 이것은 테브난의 등가저항 $R_{TH}$와 같은 방법으로 구하면 된다.

 

3) 밀만의 정리

- 내부저항을 갖는 여러개의 전압원이 병렬로 연결된 경우에 하나의 전압원 혹은 등가 전류원으로 바꾸거나 임의의 두 점 사이의 전압을 구하는데 유용한 정리.

 

 

 

예제문제

 

Q. 평면도체 표면에서 d[m]의 거리에 점전하 Q[C] 가 있을 때 전하를 무한 원점까지 운반하는데 필요한 일은 몇 [J]인가?   3

1. $\frac{Q^2}{4\pi {\epsilon }_{0}d}$

2. $\frac{Q^2}{8\pi {\epsilon }_{0}d}$

3. $\frac{Q^2}{16\pi {\epsilon }_{0}d}$

4. $\frac{Q^2}{2\pi {\epsilon }_{0}d}$

 

Q. 키르히호프 법칙에 대한 설명 중 옳지 않은 것?    3

1. 폐회로의 루프안 전압의 합은 0이다.

2. 전류가 흐르는 분기점에서의 전류의 합은 0이다.

3. 고정적인 전압/전류원이 둘 이상일 경우 사용한다.

4. 폐회로에서 기전력의 합은 전압강하의 힘과 서로 같다